Gravity wells?

[ianke]

I have a question, but first let me set up an example...

Pretend, if you will that there is a planet the same mass as earth without an atmosphere. also this planet has cooled all the way through and the core is solid. Now... This planet has a hole through it much like a pearl or a bead. Lets call this planet Pearl.

On this planet Pearl lives a man. Let us call him Earl. Earl is a short fat little guy (like me ) who weighs 100 kilograms at the surface of Pearl when he gets on his bathroom scale. Earl is a curious fellow, and decides to climb down to the center of the planet taking his bathroom scale along with him. (I didn't say Earl was bright, just curious)

As Earl climbs deaper down into Pearl, if I have this correct, when he steps onto his bathroom scale periodically he should notice that he weighs less according to the scale's reading. His Mass has not changed, but his weight should be less and less until he reaches the center of Pearl. There at the center of Pearl Earl should be weightless. Is this correct so far?

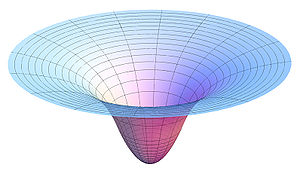
Now back to the original topic of the thread. We have all seen the 'bowling ball on the rubber sheet' depiction of gravity wells. As a whole, I see this as a good example of what gravity does to spacetime even if it is only a somewhat 2D version of the reality. For our purposes here though it will sufice perfectly. This example shows what happens outside the object quite nicely, but let us look closer at the area inside the mass that is causing the well. If the object of mass was a point scource, I would think that the bottom of the gravity well would be point shaped: however, our gravitational scource is not a point. It (planet Pearl) has dimenshion to it.

Now my questions. What would the shape of the gravity well take on the inside of our planet Pearl? I am assuming that the greatest gravitation is felt outside on the surface of the mass, and the perceived gravity is zero g at the center. If we step back and look, is it still a V shaped point? does it look flat on the bottom, or is it more like a W shape? In other words... Does spacetime stretch back out? While Earl is at the center of Pearl he feels no gravity, and since he is not free falling like an orbital object... What other anomolies would Earl likeley discover?

For instance... We know that time is slowed down by a gravitational influence, but would his watch speed back up since he is weightless? This one probably isn't correct, but if the gravity well looks sort of W shaped ( like a speaker with the center stretching back up towards the edge) perhaph his experience of spacetime may be quite different than expected.

I'll bet that I am off in left field today, but my strange mind goes strange directions sometimes. [/color]

 

[SpeedFreek]

Think of the bottom of the "well" as being at the centre of the spherical mass. The bottom of the well is flat.

You accelerate as you fall down the sides of the well, but near the bottom when you are inside the mass the slope flattens out and your acceleration slows - you weigh the most on the surface and inside the hole you weigh less and less as you approach the centre and are weightless at the centre where it is completely flat. The relationship follows the slope.

http://hyperphysics.phy-astr.gsu.edu/HB ... thole.html

 

[ianke]

Hi SpeedFreek,

And thanks for the help! This was one of the options that I had mentioned "flat at the bottom. Would you go as far as saying that the flat area is equivilant to the diameter of the object? Or... Is it more like the bottom of a parabolic curve where only the exact bottom would be considered flat? That point being the center of the object.

One other question ... At the center of a mass like the above senario, wouldn't the mass all around you effect the very fabric of spacetime in a sort of stretching or pulling force in all directions?

EDIT: After reflection on this it would most certainly be parabolic in shape. Your link was a great help with that. I still wonder what the effects on the microcosm of earl's position at the center might be like. As he is essentially at a point of zero G force, does his spacetime snap back to what it would otherwise be if no gravity well was present? He isn't exactly in a free fall like an orbiting body, so isn't he at rest with respect to the mass of the planet? It would seem to me that his position there (seeing that gravity is cancelled out) would be exactly equivilant to the planet not being there at all. Hence spacetime would be the same for him as in deep space. Time and distances for his immediate suroundings would be like the planet was not there correct?

 

[ramparts]

Hi ianke - It depends entirely on what kind of object you're talking about. In particular, it depends on the object's density profile (that is, how its mass is distributed around it). If you have an object that's densest in the inner regions, then the slope of the gravitational well will be steeper inside the object than if the object is denser on the outside. But most objects we'd consider (like the Earth, or even the Sun) come in layers and have pretty non-trivial density profiles, so the slope of the well wouldn't be something as simple as being parabolic or flat or whatever in those regions.

 

[ianke]

Hi ianke - It depends entirely on what kind of object you're talking about. In particular, it depends on the object's density profile (that is, how its mass is distributed around it). If you have an object that's densest in the inner regions, then the slope of the gravitational well will be steeper inside the object than if the object is denser on the outside. But most objects we'd consider (like the Earth, or even the Sun) come in layers and have pretty non-trivial density profiles, so the slope of the well wouldn't be something as simple as being parabolic or flat or whatever in those regions.

Hi Back at you, Rampart- Thanks for joining in. I could see where the density profile could change this quite a bit. I wasn't thinking on those lines when I started this thought experiment, but you are most certainly correct.

I guess what I am really wondering about is the point in the center, and the conditions effecting spacetime at the center of a mass, like a planet. Assuming it is symetrical, the point in the center where the gravitational pull is cancelled out seems to be an interesting spot. Much like I added in my edit above... It seems to me that due to the strange cancelling effect of the surounding mass, spacetime might be stretched back to its original shape as if the object was not there to start with. eg: spacial size would be the same as the mass not being there. Plus time would tic by as if the mass were not there. This should be true if the zero G status holds. Does this sound correct?

 

[Saiph]

the properties and behavior of space-time (and due to space-time) are indistinguishable in the center of a planet, or infinitely far away.

All that matters is the gradient (or slope) of the gravity well, not the net cause of that slope.

 

[SpeedFreek]

Gravitational time-dilation is due to the gravitational potential, rather than the gravitational force. At the centre of the Earth the gravitational potential is at its highest, so a clock at the centre would be running slow, as viewed from the surface. From the point of view of an observer at the centre of the Earth, a clock on the surface would be running fast and a clock up a mountain would be running even faster.

 

[ianke]

Thanks ramparts, Saiph, and SpeedFreek. As usual, this is the place to get great info.

 

[ramparts]

At the center of any realistic object (like the Earth) - with the sole exception of a black hole (which is entirely concentrated in the center) - there is no gravity in the exact center, so there the gravitational well is completely flat.

This is a famous result of Newton's (later shown to also work in Einstein's gravitational theory): if you are inside a sphere whose density is only a function of radius (so each shell of the sphere has constant density), the only gravitational force you feel is due to the parts of the sphere interior to you. So if you are fifty miles from the Earth's center, you'll feel the gravitational pull from every part of the Earth which is interior to a sphere of radius fifty miles, and it'll be the same pull as if all that mass were in the center. But you won't feel any gravity from the parts of the Earth that are greater than fifty miles from the center, in any direction. So obviously if you're at the center, then there's nothing interior to you, and you can't be pulled by anything, so there's no gravity.

Think on that for a bit: I think it makes intuitive sense, but it's very, very profound. That should also explain exactly why the density profile matters - because you need to know, at each distance from the planet's center, how much mass there is interior to you, and that is determined by the density profile.

 

[Jerromy]

Gravitational time-dilation is due to the gravitational potential, rather than the gravitational force.

I'm having trouble understanding this. Let us assume that Earl's twin brother Albert is sitting in a rocket on the surface of Pearl while Earl is floating in microgravity at the center of Pearl. Let us also assume they have watches that are entangled through quantum mechanics to gauge dilation instantly. I am not sure if there is an accepted convention of dilation so let us assume Earl's watch is running slower, and his gauge shows negative dilation to Albert's faster watch.
This seems backwards to me from what I remember hearing long ago of Einstein's theory of dilation. If Albert's rocket launches away from Pearl his dilation gauge should read greater positive dilation the faster he accelerates. (not faster velocity alone but faster acceleration as he excapes Pearl's gravity) If he were to continue to accelerate in a loop and return to Pearl, flying straight into the center of Pearl at nearly the speed of light, should he be older than his "twin" brother Earl since his clock has been ticking faster the entire trip?

 

[SpeedFreek]

Gravitational time-dilation is due to the gravitational potential, rather than the gravitational force.

I'm having trouble understanding this. Let us assume that Earl's twin brother Albert is sitting in a rocket on the surface of Pearl while Earl is floating in microgravity at the center of Pearl. Let us also assume they have watches that are entangled through quantum mechanics to gauge dilation instantly.

Let's stop there for a moment. Special relativity tells us that there is no absolute simultaneity, so we will have to drop the idea of measuring dilation "instantly", in any absolute sense. Also, information cannot be transmitted faster than light, even using entanglement. You can, however, set up the thought experiment with Earl and Albert using very powerful telescopes to view each others clocks.

I am not sure if there is an accepted convention of dilation so let us assume Earl's watch is running slower, and his gauge shows negative dilation to Albert's faster watch.

When Albert looks through his telescope he sees Earl's watch is running slower than his own. When Earl looks through his telescope he sees Albert's watch is running faster than his own.

This seems backwards to me from what I remember hearing long ago of Einstein's theory of dilation. If Albert's rocket launches away from Pearl his dilation gauge should read greater positive dilation the faster he accelerates. (not faster velocity alone but faster acceleration as he excapes Pearl's gravity) If he were to continue to accelerate in a loop and return to Pearl, flying straight into the center of Pearl at nearly the speed of light, should he be older than his "twin" brother Earl since his clock has been ticking faster the entire trip?

You are talking about the kinematic time-dilation described by Special Relativity, which is due to relative motion. In this thread, we are talking about gravitational time-dilation described by General Relativity, which is due to the difference in gravitational potential.

Both kinematic and gravitational time-dilation will occur in your example, but assuming Albert reaches a high enough speed, relative to Earl, the kinematic time-dilation will outweigh the gravitational time-dilation.

Let me put it this way. Consider the clock on a GPS satellite. These satellites are not geostationary, they orbit the Earth twice a day, so they are always crossing the sky and therefore have motion relative to a clock on the ground. Special Relativity predicts that the clock on the GPS satellite will run slower than a clock on the ground, by 7 microseconds a day.

But General Relativity tells us that the clock on the ground will run slower than the clock on the GPS satellite, due to the difference in gravitational potential. GR predicts that the clock on the GPS satellite will run faster than the clock on the ground, by 45 microseconds a day.

When we combine these predictions we find that the clocks on GPS satellites run faster by 38 microseconds a day, and this has been confirmed. If the GPS satellites moved faster in relation to a clock on the ground, there would come a point where the kinematic time-dilation from SR would outweigh the gravitational time-dilation from GR, and the GPS satellite clock would be running slower than a clock on Earth.

So, if Albert travels fast enough for his relative velocity to outweigh the difference in gravitational potential, his clock will run slower than a clock at the centre of the Earth.

Confusingly, kinematic time-dilation can be attributed to the force of gravity you feel, as acceleration is involved. But gravitational time-dilation is all to do with how close you are to the centre of a gravitational field, compared to someone else. It doesn't matter that you are weightless at the centre of the Earth, a clock there will "run slower" than a clock sitting on the surface of the Earth.

Gravitational potential is only zero at infinity.