Liquids in Electric Field Violate Thermodynamics

[Pentcho Valev]

Any liquid, if placed in an electric field and if no substantial current passes through it, automatically becomes a perpetuum mobile of the second kind. Vigorous jets and flows can appear, able to do mechanical work (e.g. by rotating a waterwheel) at the expense of ambient heat and in violation of the second law of thermodynamics:

View: https://www.youtube.com/watch?v=aoZnzIO9ZJ0

View: https://www.youtube.com/watch?v=aLcw1fMoc-U&t=112s

View: https://www.youtube.com/watch?v=hr76wCqq_4k


Here one can clearly see that no energy other than ambient heat can be converted into mechanical work by the liquid motion:

 

[Pentcho Valev]

When a SOLID is placed between the plates of a capacitor, the attraction between the plates INCREASES, due to polarization of the solid.

When a LIQUID is placed between the plates of the capacitor, there is polarization again but, paradoxically, the attraction between the plates DECREASES. Why? A pressure in the liquid between the plates emerges that pushes on the plates and so counteracts the original electrostatic force of attraction:

"However, in experiments in which a capacitor is submerged in a dielectric liquid the force per unit area exerted by one plate on another is observed to decrease...This apparent paradox can be explained by taking into account the DIFFERENCE IN LIQUID PRESSURE in the field filled space between the plates and the field free region outside the capacitor." http://farside.ph.utexas.edu/teaching/jk1/lectures/node46.html

The additional pressure emerging in an electric field is powered by thermal energy, like gas pressure. This means that, if suitably harnessed, the additional pressure will do work AT THE EXPENSE OF AMBIENT HEAT. Here is the molecular mechanism behind the pressure:

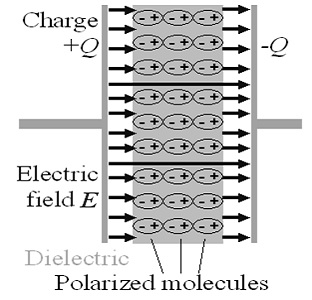
This is an idealistic polarization that would occur in the absence of thermal motion. Of course, thermal motion is always present and constantly disturbs the polarization order. The crucial point is that, as can be inferred from the picture, any thermal disturbance contributes to the creation of a local microscopic pressure. Consider a dipole that has just received a thermal stroke and has undergone rotation as a result. Now its plus end pushes an adjacent plus end and its minus end pushed an adjacent minus end. One can say, somewhat figuratively, that the dipole has absorbed heat and now, by pushing adjacent dipoles, is trying to convert the absorbed heat into work. The sum of all such microscopic disturbances is macroscopically expressed as bulk pressure.

It is this additional pressure emerging in an electric field that, under certain conditions, produces vigorous jets and flows able to do mechanical work (e.g. by rotating waterwheels) at the expense of ambient heat and in violation of the second law of thermodynamics.