S
SpeedFreek
Guest
Bob is sitting in the middle of a train carriage, and above his head is a light bulb. It emits a burst of light in all directions. When the light from that bulb reaches each end of the carriage, it causes light bulbs at each end of the carriage emit a burst of light. Bob sees that the lights at each end of the carriage flash at the same time (he has eyes in the back of his head!). A simple scenario.
But the train is passing through a station when this all happens, and Tom, who is standing on the platform, happens to be right in line with that carriage. In fact, he is right in line with the centre bulb as it flashes. But the carriage is moving in relation to him, and because of this, his view of the scene is different.
From Toms point of view, the bulb at the trailing end of the carriage flashes before the bulb at the front of the carriage.
Now Tom knows what the speed of light is, so he does the calculations to subtract the time it took for the light from the bulbs at the ends of the carriage to reach him. After doing the math, he finds that the bulb at the trailing end still flashed before the bulb at the front!
So now he calculates the light travel time from the bulb at the centre of the train to the bulb at each end. He knows that light travels at c, and that the train was moving relative to him. Once the flash of light was emitted from the centre of the train, the light propagates at c relative to Tom, but not relative to the train, from Toms point of view! As the train was moving across his view, the light actually reached the bulb at the back of the train before it reached the front.
So to Bob, the bulbs at the ends of the carriage lit up simultaneously, but to Tom they did not. Both are reality. It is not about light-travel time, it is about the constancy of the speed of light. It is not that the light from simultaneous events took different amounts of time to reach different observers, it is that the speed of light is the same to all observers, whatever their relative motions, and therefore the distance between events is not absolute across frames of reference in relative motion. Simultaneity is relative - "now", is relative. Moreover, the relativity of simultaneity works symmetrically if each observer uses the constancy of the speed of light as their reference.
If we keep the relative motion but put the bulbs on the platform instead, then in Toms frame of reference the events were simultaneous, but in Bob's frame on the train the events were not simultaneous and the difference between the events would be entirely symmetrical to when the bulbs were on the train. This shows how there is no form of absolute motion, relative to c.
Due to the constancy of c between frames in relative inertial motion, light always propagates in a sphere centred on the origin and the origin always remains at rest in relation to the observer, regardless of the motion of the source.
So, from Bob's frame, the light from the central bulb above his head propagates at 300,000 km/s in all directions relative to him, and Tom (on the platform) is moving relative to that sphere.
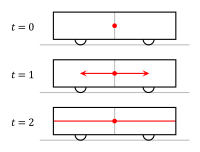
But from Toms frame, the light from the central bulb propagates from the place in space it was emitted, at 300,000 km/s in all directions relative to him, and the train with Bob on it is moving through that propagating sphere of light.
This is ultimately where (through the Lorentz contraction) we get time-dilation from, and why time-dilation is symmetrical between observers in relative inertial motion. With relative motion and increasing distance, the notion of simultaneity between two observers shifts further and further apart in a symmetrical way - each observer calculates the others clock to be time dilated by the same amount. Each observer splits up time and space differently to the other by the same amount.
So, if the shift in simultaneity is symmetrical due to relative inertial motion, when would the shift in simultaneity be asymmetrical?
But the train is passing through a station when this all happens, and Tom, who is standing on the platform, happens to be right in line with that carriage. In fact, he is right in line with the centre bulb as it flashes. But the carriage is moving in relation to him, and because of this, his view of the scene is different.
From Toms point of view, the bulb at the trailing end of the carriage flashes before the bulb at the front of the carriage.
Now Tom knows what the speed of light is, so he does the calculations to subtract the time it took for the light from the bulbs at the ends of the carriage to reach him. After doing the math, he finds that the bulb at the trailing end still flashed before the bulb at the front!
So now he calculates the light travel time from the bulb at the centre of the train to the bulb at each end. He knows that light travels at c, and that the train was moving relative to him. Once the flash of light was emitted from the centre of the train, the light propagates at c relative to Tom, but not relative to the train, from Toms point of view! As the train was moving across his view, the light actually reached the bulb at the back of the train before it reached the front.
So to Bob, the bulbs at the ends of the carriage lit up simultaneously, but to Tom they did not. Both are reality. It is not about light-travel time, it is about the constancy of the speed of light. It is not that the light from simultaneous events took different amounts of time to reach different observers, it is that the speed of light is the same to all observers, whatever their relative motions, and therefore the distance between events is not absolute across frames of reference in relative motion. Simultaneity is relative - "now", is relative. Moreover, the relativity of simultaneity works symmetrically if each observer uses the constancy of the speed of light as their reference.
If we keep the relative motion but put the bulbs on the platform instead, then in Toms frame of reference the events were simultaneous, but in Bob's frame on the train the events were not simultaneous and the difference between the events would be entirely symmetrical to when the bulbs were on the train. This shows how there is no form of absolute motion, relative to c.
Due to the constancy of c between frames in relative inertial motion, light always propagates in a sphere centred on the origin and the origin always remains at rest in relation to the observer, regardless of the motion of the source.
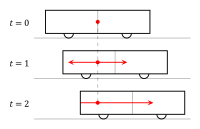
So, from Bob's frame, the light from the central bulb above his head propagates at 300,000 km/s in all directions relative to him, and Tom (on the platform) is moving relative to that sphere.

But from Toms frame, the light from the central bulb propagates from the place in space it was emitted, at 300,000 km/s in all directions relative to him, and the train with Bob on it is moving through that propagating sphere of light.

This is ultimately where (through the Lorentz contraction) we get time-dilation from, and why time-dilation is symmetrical between observers in relative inertial motion. With relative motion and increasing distance, the notion of simultaneity between two observers shifts further and further apart in a symmetrical way - each observer calculates the others clock to be time dilated by the same amount. Each observer splits up time and space differently to the other by the same amount.
So, if the shift in simultaneity is symmetrical due to relative inertial motion, when would the shift in simultaneity be asymmetrical?


