All consequences of the second law of thermodynamics are preposterous but the champion is undoubtedly the proposition that catalysts accelerate the forward and backward reactions "equally" or "by the same factor":
"Suppose that, as indicated in the figure, the catalyst affects only the forward reaction. In its presence, the sum of the forward rates would clearly be larger than otherwise, while the backward rate would be unchanged. The position of equilibrium would therefore shift to the right, by the law of mass action. If we suppose further that the reaction produces heat q when it occurs, then a violation of the second law would be possible. We first allow equilibrium to be reached without the catalyst...and then add the catalyst, and heat δq is produced as the equilibrium is shifted. This heat is used to run a machine, and thus do work, cooling the system back to its original temperature in the process. We then remove the catalyst and the equilibrium shifts back. Heat δq is now extracted from the surroundings, which must warm the system back to the ambient temperature. A cycle has therefore been completed for which the net effect has been the isothermal conversion of heat energy into work, and a perpetual motion machine of the second kind has been found. We conclude that the supposed situation is impossible and that the catalyst must accelerate the forward and backward reactions equally." https://dtk.tankonyvtar.hu/bitstream/handle/123456789/8903/B9780120442621500128.pdf
"It is important to recognize that when an enzyme (or any catalyst) lowers the activation energy for the reaction A → B, it also lowers the activation energy for the reaction B → A by exactly the same amount (see Figure 2-44). The forward and backward reactions will therefore be accelerated by the same factor by an enzyme..." https://www.ncbi.nlm.nih.gov/books/NBK26838/
"Equally" ("by the same factor") is in flagrant contradiction with reality:
"The protein scaffold around an enzyme’s catalytic core exquisitely controls reactivity, including the direction and rate of chemical processes. Scientists refer to this fine tuning as “catalytic bias”—and how it occurs remains widely debated...A research team from three U.S. Department of Energy (DOE) national laboratories and four universities found that subtle changes to the environment surrounding some enzymes can not only change the rate of a cellular reaction by a staggering six orders of magnitude but also its direction. That reversal—the root of the catalytic bias dilemma—is like speeding in one direction at 10 miles-per-second, then going in the opposite direction at 1,000,000 miles-per-second." https://www.pnnl.gov/news-media/remarkable-rate-return-catalytic-bias
"Interestingly, although [FeFe]-hydrogenases all possess the same active site H cluster, they display a large range of H2 gas oxidation and proton reduction activities, with some displaying a dramatic catalytic bias, that is, the propensity of a catalyst to effect rate of acceleration in one reaction direction over the other. " https://europepmc.org/article/pmc/pmc8653774
"This has resulted in a deeper understanding of the hydrogenase model system and the ability to directly influence catalytic bias. Thus, the work presented here represents key progress towards developing unidirectional catalysts, and demonstrates the possibility of targeted, rational design and implementation of unidirectional catalysts." https://scholarworks.montana.edu/xmlui/handle/1/14621
"However, many enzymes reversibly convert their substrate and product, and if one is interested in catalysis in only one direction, it may be necessary to prevent the reverse reaction...This is the first demonstration, on a specific example, that slowing a step that is rate limiting only when the enzyme works in one direction is a general mechanism for biasing the enzyme in the other direction." https://hal.science/hal-01977597/document
Scientists should have exposed the absurdity of
"Catalysts accelerate the forward and reverse reactions equally, by the same factor"
long ago, and should have applied reductio ad absurdum: Since the consequence is absurd, the underlying premise, the second law of thermodynamics, is false.
Consider the dissociation-association reaction
A ⇌ B + C
which is in equilibrium. We add a catalyst and it starts splitting A - the rate constant of the forward (dissociation) reaction increases by a factor of, say, 745492. If the second law of thermodynamics is obeyed, the catalyst must increase the rate constant of the reverse (association) reaction by exactly the same factor, 745492. But this is insane! The reverse reaction is entirely different from the forward one: B and C must first get together, via diffusion, and only then can the catalyst join them to form A. Catalysts don't speed up diffusion! And if diffusion is the rate-limiting step of the reverse reaction (that is, the reverse reaction is diffusion-controlled), the catalyst is unable to accelerate B+C→A at all!
That catalysts do not accelerate the forward and reverse reactions "equally" was my first heretical idea, about 30 years ago. Journals used to reject my submissions, as it were, before receiving them. As far as I remember, the editors of Nature (Philip Ball was the godfather among them) were the most adamant. The irony is that, later, in 2013, they published a paper describing a more than obvious violation of the second law. Far from accelerating the forward and backward reactions "equally" ("by the same factor"), in this experiment
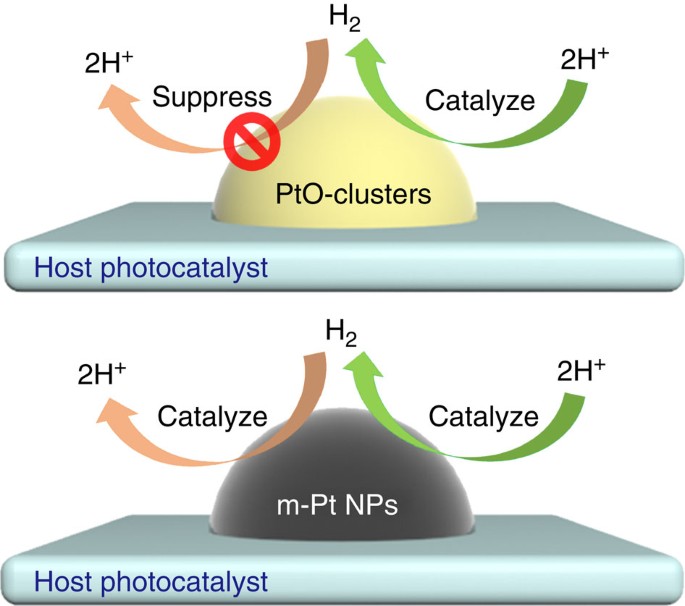
Yu Hang Li et al. Unidirectional suppression of hydrogen oxidation on oxidized platinum clusters https://www.nature.com/articles/ncomms3500
the catalyst, PtO, accelerates only 2H+ → H_2, the forward reaction, and SUPPRESSES H_2 → 2H+, the backward reaction:
"Suppose that, as indicated in the figure, the catalyst affects only the forward reaction. In its presence, the sum of the forward rates would clearly be larger than otherwise, while the backward rate would be unchanged. The position of equilibrium would therefore shift to the right, by the law of mass action. If we suppose further that the reaction produces heat q when it occurs, then a violation of the second law would be possible. We first allow equilibrium to be reached without the catalyst...and then add the catalyst, and heat δq is produced as the equilibrium is shifted. This heat is used to run a machine, and thus do work, cooling the system back to its original temperature in the process. We then remove the catalyst and the equilibrium shifts back. Heat δq is now extracted from the surroundings, which must warm the system back to the ambient temperature. A cycle has therefore been completed for which the net effect has been the isothermal conversion of heat energy into work, and a perpetual motion machine of the second kind has been found. We conclude that the supposed situation is impossible and that the catalyst must accelerate the forward and backward reactions equally." https://dtk.tankonyvtar.hu/bitstream/handle/123456789/8903/B9780120442621500128.pdf
"It is important to recognize that when an enzyme (or any catalyst) lowers the activation energy for the reaction A → B, it also lowers the activation energy for the reaction B → A by exactly the same amount (see Figure 2-44). The forward and backward reactions will therefore be accelerated by the same factor by an enzyme..." https://www.ncbi.nlm.nih.gov/books/NBK26838/
"Equally" ("by the same factor") is in flagrant contradiction with reality:
"The protein scaffold around an enzyme’s catalytic core exquisitely controls reactivity, including the direction and rate of chemical processes. Scientists refer to this fine tuning as “catalytic bias”—and how it occurs remains widely debated...A research team from three U.S. Department of Energy (DOE) national laboratories and four universities found that subtle changes to the environment surrounding some enzymes can not only change the rate of a cellular reaction by a staggering six orders of magnitude but also its direction. That reversal—the root of the catalytic bias dilemma—is like speeding in one direction at 10 miles-per-second, then going in the opposite direction at 1,000,000 miles-per-second." https://www.pnnl.gov/news-media/remarkable-rate-return-catalytic-bias
"Interestingly, although [FeFe]-hydrogenases all possess the same active site H cluster, they display a large range of H2 gas oxidation and proton reduction activities, with some displaying a dramatic catalytic bias, that is, the propensity of a catalyst to effect rate of acceleration in one reaction direction over the other. " https://europepmc.org/article/pmc/pmc8653774
"This has resulted in a deeper understanding of the hydrogenase model system and the ability to directly influence catalytic bias. Thus, the work presented here represents key progress towards developing unidirectional catalysts, and demonstrates the possibility of targeted, rational design and implementation of unidirectional catalysts." https://scholarworks.montana.edu/xmlui/handle/1/14621
"However, many enzymes reversibly convert their substrate and product, and if one is interested in catalysis in only one direction, it may be necessary to prevent the reverse reaction...This is the first demonstration, on a specific example, that slowing a step that is rate limiting only when the enzyme works in one direction is a general mechanism for biasing the enzyme in the other direction." https://hal.science/hal-01977597/document
Scientists should have exposed the absurdity of
"Catalysts accelerate the forward and reverse reactions equally, by the same factor"
long ago, and should have applied reductio ad absurdum: Since the consequence is absurd, the underlying premise, the second law of thermodynamics, is false.
Consider the dissociation-association reaction
A ⇌ B + C
which is in equilibrium. We add a catalyst and it starts splitting A - the rate constant of the forward (dissociation) reaction increases by a factor of, say, 745492. If the second law of thermodynamics is obeyed, the catalyst must increase the rate constant of the reverse (association) reaction by exactly the same factor, 745492. But this is insane! The reverse reaction is entirely different from the forward one: B and C must first get together, via diffusion, and only then can the catalyst join them to form A. Catalysts don't speed up diffusion! And if diffusion is the rate-limiting step of the reverse reaction (that is, the reverse reaction is diffusion-controlled), the catalyst is unable to accelerate B+C→A at all!
That catalysts do not accelerate the forward and reverse reactions "equally" was my first heretical idea, about 30 years ago. Journals used to reject my submissions, as it were, before receiving them. As far as I remember, the editors of Nature (Philip Ball was the godfather among them) were the most adamant. The irony is that, later, in 2013, they published a paper describing a more than obvious violation of the second law. Far from accelerating the forward and backward reactions "equally" ("by the same factor"), in this experiment
Yu Hang Li et al. Unidirectional suppression of hydrogen oxidation on oxidized platinum clusters https://www.nature.com/articles/ncomms3500
the catalyst, PtO, accelerates only 2H+ → H_2, the forward reaction, and SUPPRESSES H_2 → 2H+, the backward reaction:



