"A plane capacitor with rectangular plates is fixed in a vertical position...The capacitor is charged and disconnected from the battery...The lower part of the capacitor is now brought into contact with a dielectric liquid [e.g. deionized water]...When the plates contact the liquid's surface, a force in the upward direction is exerted on the dielectric liquid. The total charge on each plate remains constant." http://electron6.phys.utk.edu/PhysicsProblems/E&M/2-Dielectrics/capacitors_with_dielectrics.html

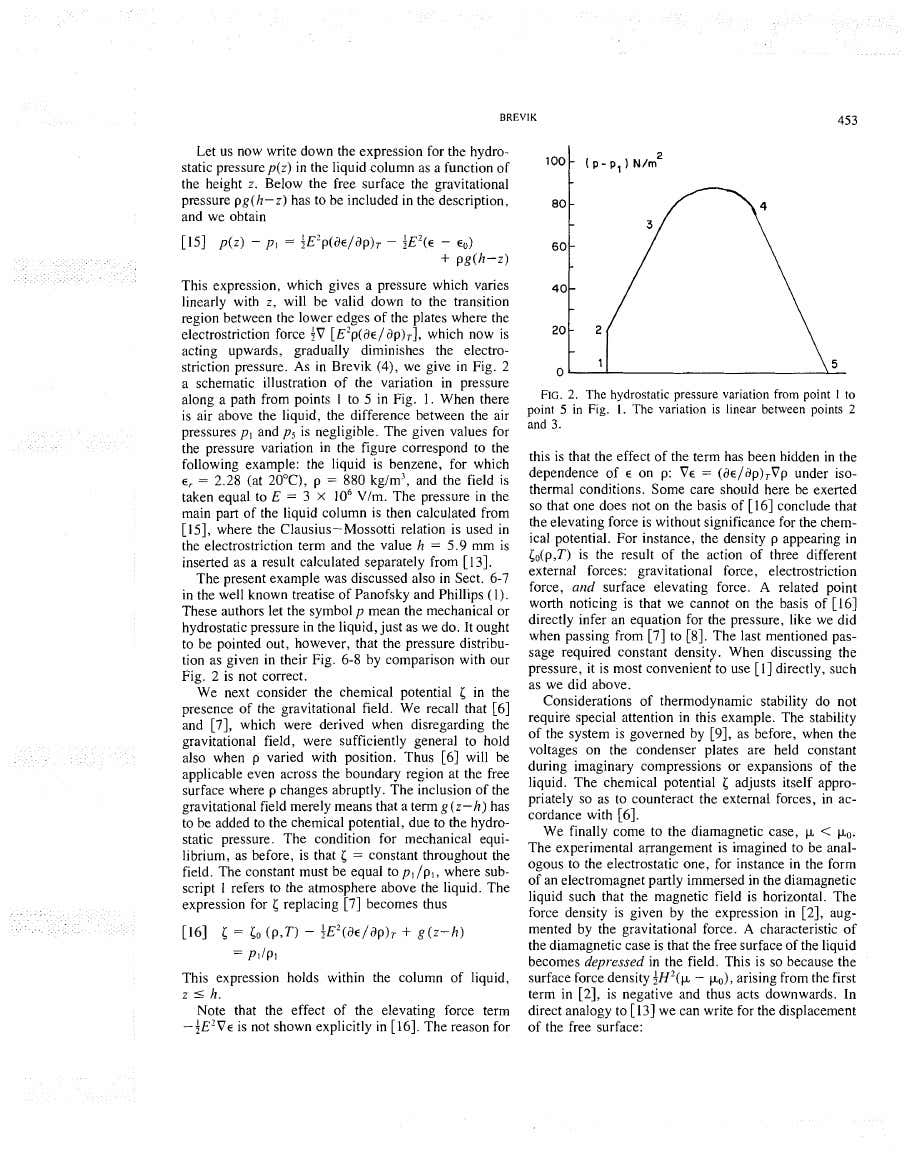
In an electric field, water develops a specific bulk pressure that pushes in all directions and can, as in the above case, lift the water against the gravitational force:
"However, in experiments in which a capacitor is submerged in a dielectric liquid the force per unit area exerted by one plate on another is observed to decrease...This apparent paradox can be explained by taking into account the DIFFERENCE IN LIQUID PRESSURE in the field filled space between the plates and the field free region outside the capacitor." http://farside.ph.utexas.edu/teaching/jk1/lectures/node46.html
The pressure is NON-CONSERVATIVE. This means that, if suitably harnessed, it will do work AT THE EXPENSE OF AMBIENT HEAT and in violation of the second law of thermodynamics. Here is the molecular mechanism:
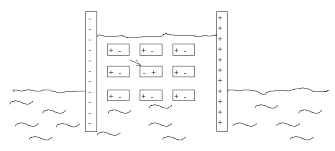
If it were not for the indicated (with an arrow) dipole, other dipoles in the picture are perfectly polarized as if there were no thermal motion. Of course, this is an oversimplification – thermal motion is a factor which constantly disturbs the polarization order. The crucial point is that, as can be inferred from the picture, any thermal disturbance contributes to the creation of a local microscopic pressure. Consider the indicated dipole. It has just received a thermal stroke and has undergone rotation as a result. Now it pushes adjacent dipoles electrostatically. One can say, somewhat figuratively, that the indicated dipole has absorbed heat and now, by pushing adjacent dipoles, is trying to convert the absorbed heat into work.
The sum of all such microscopic disturbances is macroscopically expressed as bulk pressure. Systems of this kind can convert ambient heat into work, in violation of the second law of thermodynamics.

In an electric field, water develops a specific bulk pressure that pushes in all directions and can, as in the above case, lift the water against the gravitational force:
"However, in experiments in which a capacitor is submerged in a dielectric liquid the force per unit area exerted by one plate on another is observed to decrease...This apparent paradox can be explained by taking into account the DIFFERENCE IN LIQUID PRESSURE in the field filled space between the plates and the field free region outside the capacitor." http://farside.ph.utexas.edu/teaching/jk1/lectures/node46.html
The pressure is NON-CONSERVATIVE. This means that, if suitably harnessed, it will do work AT THE EXPENSE OF AMBIENT HEAT and in violation of the second law of thermodynamics. Here is the molecular mechanism:
If it were not for the indicated (with an arrow) dipole, other dipoles in the picture are perfectly polarized as if there were no thermal motion. Of course, this is an oversimplification – thermal motion is a factor which constantly disturbs the polarization order. The crucial point is that, as can be inferred from the picture, any thermal disturbance contributes to the creation of a local microscopic pressure. Consider the indicated dipole. It has just received a thermal stroke and has undergone rotation as a result. Now it pushes adjacent dipoles electrostatically. One can say, somewhat figuratively, that the indicated dipole has absorbed heat and now, by pushing adjacent dipoles, is trying to convert the absorbed heat into work.
The sum of all such microscopic disturbances is macroscopically expressed as bulk pressure. Systems of this kind can convert ambient heat into work, in violation of the second law of thermodynamics.
Last edited: