Where is the centre point of the universe

[RobbyQbit]

The one thing I struggle with is where was the centre of the Big Bang and is there a centre point in the universe or is BB the centre ? It's easy to think that we sat here on Earth are at the centre. But that isn't the case. How do you visualise this yourselves? Is there actually a centre point and if not, why not? Is the BB like an explosion that the centre of origin can be pin pointed?

 

[billslugg]

There is no one central point in the Universe. Every point in the Universe sees the density of galaxies the same in every direction. Every point in the Universe sees itself as at the central point.

The BB was not an explosion of matter but was an explosion of space.

There is, however, a preferred velocity. We can see ourselves moving through space, in a certain direction , simply by looking at where the CMBR is blue shifted.

 

[Koos Roegholt]

The center is not in the universe. It lies at the center of the 4-d sphere of which the 3-d universe is the (curved) surface.

 

[RobbyQbit]

The BB was not an explosion of matter but was an explosion of space.

Of course, matter did not exist then. But what is the definition of space. What actually is space. Physically, what is space?

There is, however, a preferred velocity. We can see ourselves moving through space, in a certain direction , simply by looking at where the CMBR is blue shifted.

Blue shifted being the stuff approaching us?

 

[RobbyQbit]

There is no one central point in the Universe. Every point in the Universe sees the density of galaxies the same in every direction. Every point in the Universe sees itself as at the central point.

And there's the rub Bill. Every point in the Universe sees itself as at the central point.

 

[billslugg]

Yes, in three spatial dimensions there is no one center to the Universe.
An analogy is spots on a balloon as it expands, no one center to the surface there either.

 

[Helio]

The ant on an expanding balloon, if told to find the center of the balloon somewhere on the surface would not ever find one. Shrinking the balloon would also not help.

As I see it, so perhaps I'm wrong, the extreme density of a very young universe bends space so much that no matter which direction one choses to go to find an "edge" the traveler will travel a path that only looks straight, but is constantly bent, thus there is no edge, and no center.

 

[Helio]

And there's the rub Bill. Every point in the Universe sees itself as at the central point.

Yes, but I would rephrase it to be "appears to be at a central point".

 

[billslugg]

An observer is only at the central point from their perspective. It will not appear this way to anyone else. And it does not just appear that way to an observer, it is that way.

 

[Helio]

An observer is only at the central point from their perspective. It will not appear this way to anyone else. And it does not just appear that way to an observer, it is that way.

Apparently so.

 

[Classical Motion]

If you believe space came with mass, and that our time space is on a curve of expanding space.......then all you have to do is measure the curve.......and that will tell you where the center is.

Good luck.

 

[billslugg]

The problem is when we look out there as far as we can see, it all looks the same. Same types and same numbers of galaxies in every direction, same recessional velocities. Same everything. CMBR is slightly different but only by a ppm or so. That tells us we are moving through space, but space itself looks the same in every direction.

 

[Atlan0001]

Every point of the universe is the 0-point-center of the spherical dome, thus a universe of infinite points and infinite horizons. But only one (closed up to the Horizon) universal Horizon [set] of all the infinities of horizon universes.

What of the famous ant standing on the famous surface of that famous sphere, quantum entangled in two places at once as also being at the 0-point-center of its horizon sphere . . . as usual to surface horizons of spheres like Earth's horizon where everything on the surface is always inside that horizon and always outside of it always distant from it (a quantum entanglement) all at the same time? Where is the infinity regarding that ant when it stands on the surface of the sphere?

It travels a changing world forever toward the merging timelines of longitude at the poles, the points, and never leaves the equator. Well, in fact that is not quite true, for the ant is all over the surface of the sphere, everywhere in, on, the Horizon, all at once in being quantum entangled with it (Heisenberg uncertainty principle-like (the finite '1' (unity) being every bit the equal of the infinite '0' (null unity) in fundamental binary base2)). Fractal zoom structure set and reset. Square matrix (eigenvector). An endless frontier with the closed-up Horizon (in reduction to an endless universal constant of beginning) of all of an infinity of horizon universes always on the Horizon. To expand upon what I just said . . . or to reduce it, no one is NOT the center of the universe! Everyone is the center! Live with it!

 

[Rorisang]

The one thing I struggle with is where was the centre of the Big Bang and is there a centre point in the universe or is BB the centre ? It's easy to think that we sat here on Earth are at the centre. But that isn't the case. How do you visualise this yourselves? Is there actually a centre point and if not, why not? Is the BB like an explosion that the centre of origin can be pin pointed?

The concept of the "center" of the Big Bang and the universe is a bit tricky and can be counterintuitive. To understand this, you have to shift your perspective because the Big Bang was not an explosion that occurred at a specific point in space. Instead, it was an expansion of the entire universe from an extremely hot and dense state.

Think of it in this way

1. No Center in Space: The Big Bang didn't happen at a single point in space. Instead, the universe was compressed into an incredibly tiny and hot state. As it expanded, it did so uniformly in all directions. So, there's no one point you can pinpoint as the "center" of the explosion.

2. Expansion of Space: Imagine the universe as a balloon. When you blow up the balloon, it doesn't expand from a specific point on the surface; rather, the entire surface expands uniformly. Similarly, the universe expanded from a highly dense state, and all points in space moved away from each other.

3. Observable Universe:What we observe as the observable universe is a sphere centered on us. This is because light from distant objects takes time to reach us, and the universe is roughly 13.8 billion years old. We see the universe as it was when the light from those distant objects was emitted. So, the observable universe has a spherical boundary centered on our point of observation, but this doesn't mean the entire universe has a center.

4. Cosmic Microwave Background (CMB):The CMB is a faint radiation that fills the universe. It is nearly uniform in all directions and provides evidence for the Big Bang. Its uniformity supports the idea that the universe doesn't have a central point of origin.

In summary, the Big Bang was not like a conventional explosion with a single point of origin. It was an expansion of the universe from an extremely dense state, and from our perspective, it appears as though everything is moving away from us. However, this is true for all observers in the universe, and there is no universal center.

Visualizing this concept can be challenging, but analogies like the expanding balloon can help you understand that the universe's expansion is a property of space itself and not a conventional explosion from a point.

 

[7icarus7]

Regarding the center of the universe, there are differences in the coordinate system used between physicists and the public.

When physicists describe the universe, they describe it in 4-dimensional space including the dimension of curvature, or 4-dimensional spacetime including the dimension of time. However, public think in 3-dimensional space (Movement over time in three dimensions of space. Newtonian mechanical world view).

In the problem related to the center of the universe, because the center of a 4-dimensional space exists in the 4th dimension (because it requires 4 coordinates), the center does not exist in the 3-dimensional space that public see. This is also why physicists use the analogy of a balloon or a raisin in bread.

Therefore, physicists always say that the center of the universe does not exist (in the 3-dimensional space we see).

On the other hand, it is difficult for the public to understand and agree with physicists' claims because we can define the center by looking at a 3-dimensional sphere.

Where is the center of the observable universe?

If the observable universe is described in 3 dimensions, the center is me (or Earth), and if the observable universe is described in 4 dimensions, everywhere is not the center. An event depends on the coordinate system it describes.

The public asks in 3D space, and physicists answer in 4D space or 4D spacetime(or 3+1 dimension).

However, there are three things that make physics great, one is assumption, another is approximation, and the last one is experiment. This is because complex real-world phenomena can be simplified through assumption and approximation, and once they reach a level where they are sufficiently useful in reality, that alone is valuable.

In the first place, approximations have meaning because all values, including physical constants, are strictly approximations, and the tools that measure them themselves have measurement errors.

Regardless of whether 4D space including curvature is an accurate description, it is necessary to think about whether this can be approximated in 3D space. Observations of the universe show that space is nearly flat, which suggests that the fourth dimension of curvature can be ignored or approximated (depending on the accuracy required).

It is estimated that the current universe would be meaningful even if it were described in 3-dimensions.

Now, if we describe the universe as having three spatial dimensions, it is very likely that the center of the universe will lie within the three-dimensional mass distribution. Moreover, gravity is an attractive force, and when a repulsive force exists on a cosmic scale, the repulsive force is likely to be of a type that depends on r.

F=-G(-M)m/r^2 = -G(-(4/3)πr^3ρ)m/r^2 = +(4πGρ/3)r

When this repulsive or anti-gravity force exists, the universe can expand into a uniform sphere.

If the mass distribution in the entire universe is not infinite, the center of the 3D mass distribution must exist in 3D, and we can find its location. However, if the entire universe is infinite, there is no center.

[How to find the 3D space center of the entire universe]

If we extrapolate from the Hubble-Lemaître law,

1)We observe the red-shift of all galaxies that are a certain distance r from the Earth. The observed galaxies lie on the surface of a sphere of radius r.

2)Due to various factors, there will be errors in red-shift. From this data, find the plane (or circumference) with the smallest red-shift error.

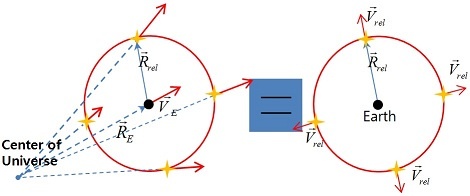
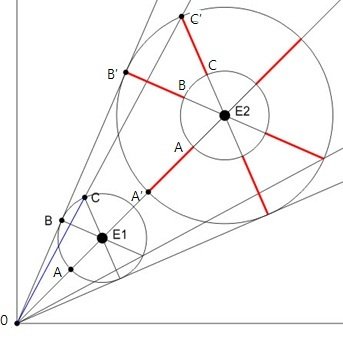
So that all of the red lines are the same size. It’s important also that the lengths are proportional, so for example E_2A’/E_1A is equal to E_2B’/E_1B and E_2C’/E_1C since recession velocity from the center needs to be proportional to distance.

E_2A’/E_1A=E_2B’/E_1B=E_2C’/E_1C

V_rel=HD

This is the Hubble-Lemaître law.

3)The 3D space center of the entire universe exists in the direction perpendicular to the plane where the redshift error value is the smallest.

Because the entire universe is larger than the observable universe, it is possible that the three-dimensional space center of the entire universe exists outside the observable universe.

If the mass distribution in the universe is finite, we need to find the 3D space center of the universe and establish an absolute coordinate system (or center of mass coordinate system).

 

[Atlan0001]

That every point of the universe is o-point-center is not based on geometry. It based upon two things, an infinity of 0-point-centers, and the same set Horizon for every one of those infinity of centers, themselves thus an infinity of horizons (to that set) out from the infinity of other points broad and deep. The multi-dimensional MULTIVERSE, which includes all the dimensions of quantum physics and quantum weirdness . . . all the dimensions of the microcosm, the micro-microcosm, the macrocosm, the macro-macrocosm, the fractal zooms structure of the universe, the eigenvector or square matrix structure of the universe, the fine structure constant, the times before times, the times after times, all the multiplicity of points of the past and future cones, the matter of antimatter, the energies positive and negative.... and much more.

Each one of us humans and aliens on Earth is a moving center of the universe, along with the Earth itself, our Milky Way galaxy itself, and we move those countless many horizons with all our own movements as does every point of movement within each of us. Based on everything in it, our universe may be just one of many discreet quanta bubbles, all of them in movement crossing, possibly coming into friction, and even colliding. Thus, it is being claimed that the universe, and us with it, can be nothing more in fact than holographic simulation because the dimensionality is simply too vast, too complex, too chaotic, too weird, too imaginative to pin down to anything like just four boxed-in dimensions. Funny as it may seem, if it's a holographic simulation, it puts us, each one of us, along with everything else of it on an even, equal, basis with the whole thing altogether . . . just another form of centering.

 

[Atlan0001]

In other threads I have not made a mistake talking a dimension of "asymptote" between curvatures of the universe. It is what astrophysicist astronomers think of -- when they think at all -- of the astronomy of the observable universe they look to when looking into and through their scopes.

But it's a multi-dimensional universe, folks, with multi-dimensional curvatures to it. I describe a line of "asymptote" in one dimensionality that is in fact a titanic curvature that astronomers are looking into now that they are missing very badly. Once more the geometry of the "Klein bottle" to illustrate it and give astronomers, cosmologists, and astrophysicists a clue about what they are in fact looking at:

Klein bottle - Wikipedia

en.wikipedia.org

Astronomers are looking up and out into a titanic dimension (titanic geometry) of curvature of universe that curves up, up, and out until it curves down, down, and in toward the Planck Horizon of the universe inside the very detectable microcosmic physics. arrived at their scopes. It is an asymptotic curvature they are trying so very hard not to see or understand. Not two points of horizon at a distance out apart but two points of horizon at a distance in-depth apart (apart within) occupying the same 0-point-center at once . . . every 0-point-center of an infinity of 0-point centers at once (at one and the same time, toward and nearing the collapsed cosmological constant (/\) of the Planck Horizon).

You can look at the cone (the curvature) from the big end to the small end of the cone (the curvature) or from the small end to the big end of the cone (the curvature), ending up always, inevitably, at / in the same 0-point center of the universe(s).