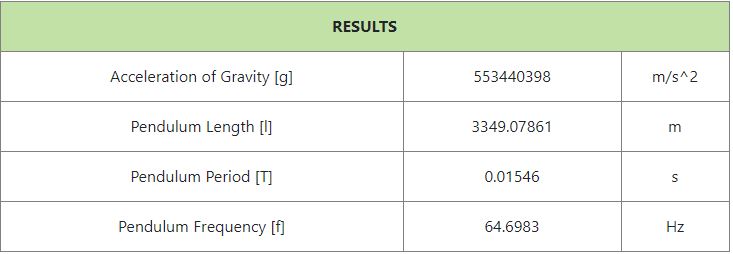
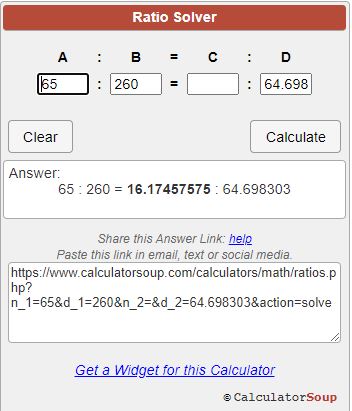
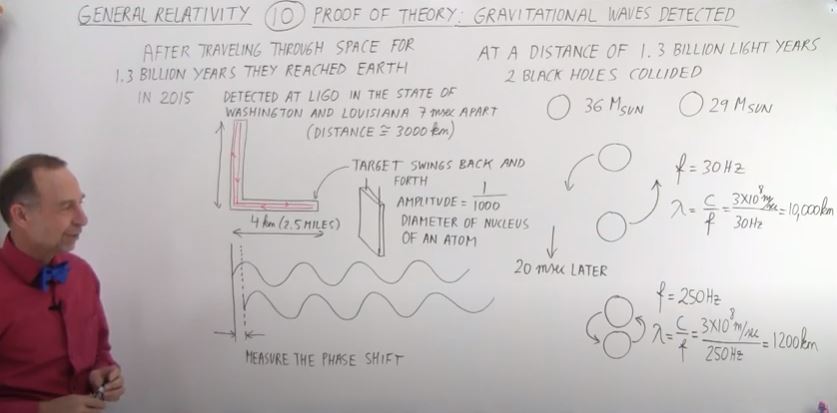
I bolded and underlined the main calculations that fit the above Pendulum Calculation.
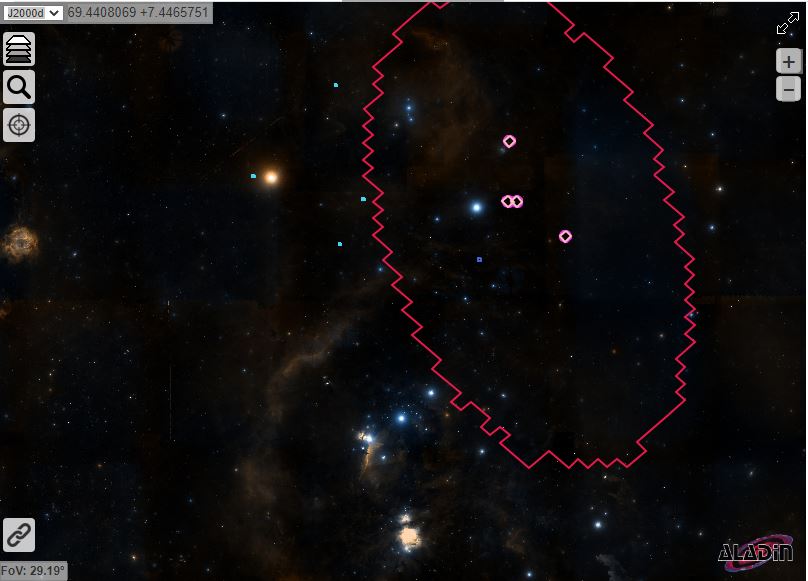
Here the information from the Grace Database at Ligo:
| Group | Burst |
| Detectors | H1,L1,V1 |
| Time of Signal | 2020-01-14 02:08:18.230000 UTC |
| Time Sent | 2020-01-14 02:48:21 UTC |
| False Alarm Rate | once per 25.84 years |
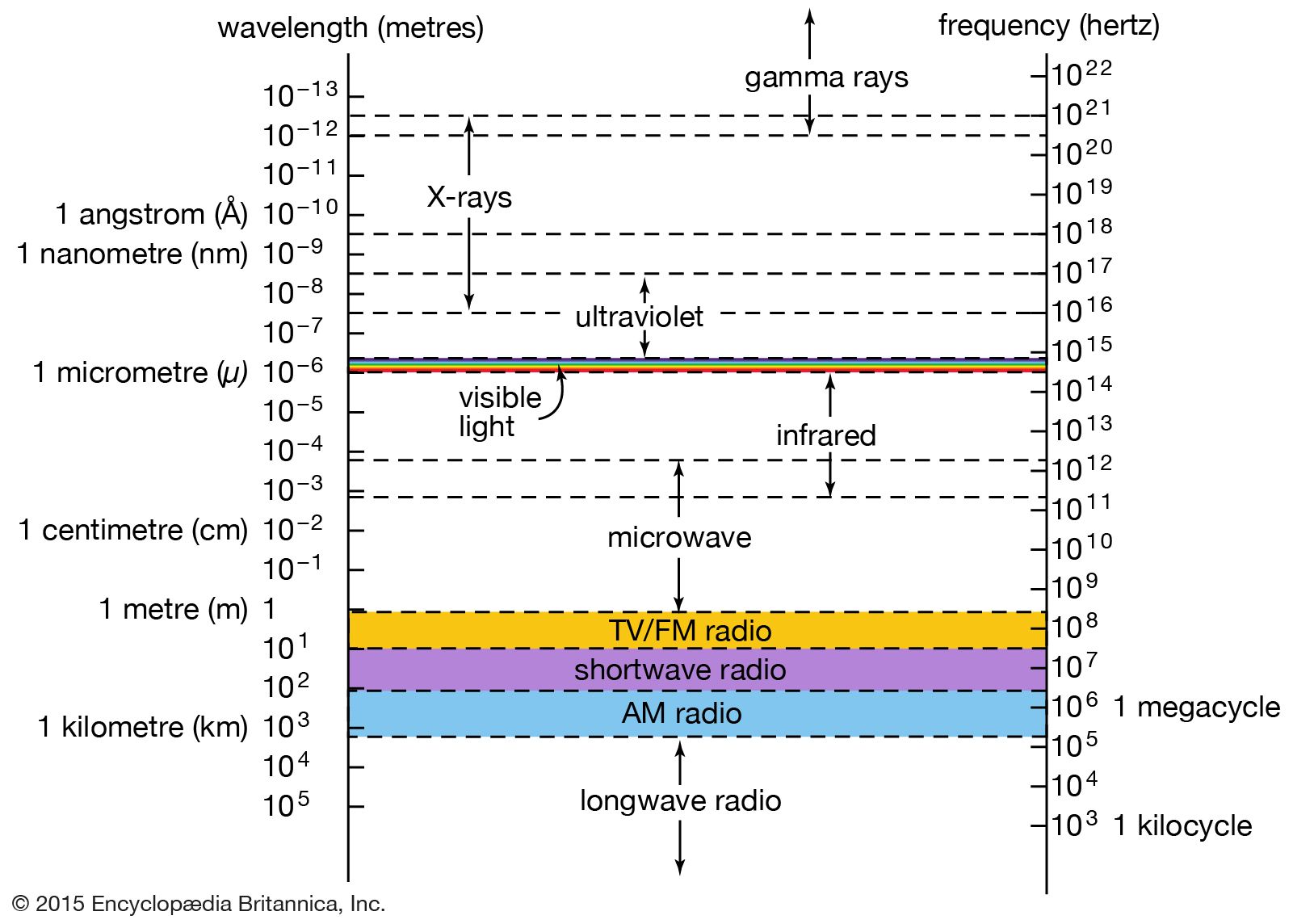
| Central Frequency | 64.698303 Hz |
| Duration | 0.013534 seconds |
treasuremap.space
Here is the data from the masses of Earth compared to Betelgeuse to obtain gravitational force:
Enter weight of first body Betelgeuse (Kg): 34806000000000000000000000000000
Enter weight of second body Earth(Kg): 5972000000000000000000000
Enter distance (m): 5006620000000000000 Distance from Earth to Betelgeuse
34806000000000000000000000000000 Weight of First Body Kg
5972000000000000000000000 Weight of Second Body Kg
553440398.5241719484329223632812500000000000000000000000000000000000000000000000000000000000000000000000000000 Gravitational Force
0.00000000006674 Gravitational Constant
Here is the information from my Gravity Geometric which matches up with the Pendulum all bold and underline is in the Pendulum:
Enter Number to divide Proton:
3349
Spin Number: .799
Enter number of Parsec's for Luminosity Distance: 150
Add Parsec's for Luminosity Distance: 19
Subtract Parsec's for Luminosity Distance: 5
0.00000000006674 Gravitational Constant
2.0000000000000027 G as exponential growth
6.280000000000008 Gravities_Geometry
534.64 Ligos distance approximation from luminosity in light years
529.2 Distance Gravity Wave traveled going by ONeils Gravity Geometric
5.422732819268049 difference from Ligo and Geometric source in light years
00:00:00
Mass to Gravitational Force Calculation in Python:
Python:
# Python Program to Calculate Gravitational Force
# setting value of Gravitational Constant
# Reading weight and distance
while True:
G = (.00000000006674)
m1 = int(input('Enter weight of first body (Kg): '))
m2 = int(input('Enter weight of second body (Kg): '))
r = int(input('Enter distance (m): '))
# Calculating Gravitational Force
F = (((G * m1) * m2) / r**2)
# Displaying result
print(m1,'Weight of First Body Kg')
print(m2,'Weight of Second Body Kg')
print('{0:.100f}'.format(F),'Gravitational Force')
print('{0:.14f}'.format(G),'Gravitational Constant')
My Gravity Wave Geometric Calculation Python:
Python:
import time
print('''Two to the power of Exponential growth of Gravities
Constant <G> multiplied by the fine structure contant multiplied
by 12 hours divided by n.
________________________________________ ''')
while True:
n = int(input("Enter Number to divide Proton: "))
s = float(input("Spin Number: "))
Parsec = int(input("Enter number of Parsec's for Luminosity Distance: "))
Plus_Parsec = int(input("Add Parsec's for Luminosity Distance: "))
Minus_Parsec = int(input("Subtract Parsec's for Luminosity Distance: "))
start_time = time.time()
G_constant = (.00000000006674)
proton_width = (((0.00000000000001)*s)/(n))
gravity_wave = ((proton_width))
G = ((pow(2,((1 +(((.00000000006674*.0072973*(12/n))*((( 1 ))))))))))
Gravities_Geometry = ((G*3.14))
Distance_to_Gravity_Waves_Source = (((((((G))/(gravity_wave))*86400*365)/((Gravities_Geometry)-((G/2))))/9461000000000000))/1000000
Ligos_approximation_Black_hole_merger_from_luminosity = (3.26*(Parsec+(Plus_Parsec-Minus_Parsec)))
difference = (Ligos_approximation_Black_hole_merger_from_luminosity-Distance_to_Gravity_Waves_Source)
print('{0:.14f}'.format(G_constant),'Gravitational Constant')
# print('{0:.99f}'.format(proton_width),'Proton Width')
# print('{0:.110f}'.format(gravity_wave),'Gravity Wave')
print(G,'G as exponential growth')
print('{0:.15f}'.format(Gravities_Geometry),'Gravities_Geometry')
print("{:,}".format(Ligos_approximation_Black_hole_merger_from_luminosity),'Ligos distance approximation from luminosity in light years')
print('{0:,.1f}'.format(Distance_to_Gravity_Waves_Source),'Distance Gravity Wave traveled going by ONeils Gravity Geometric')
print("{:,}".format(difference),'difference from Ligo and Geometric source in light years')
e = int(time.time() - start_time)
print('{:02d}:{:02d}:{:02d}'.format(e // 3600, (e % 3600 // 60), e % 60))
courses.lumenlearning.com