On January 14, 2020 the folks at Ligo Laser Interferometer Labs reported a mysterious gravity wave which does not fit the normal signature of a Black Hole merger nor a Neutron Star Black Hole Merger. Some have suggested the signature gravity wave may very well have been a Supernova event, because of its short duration.
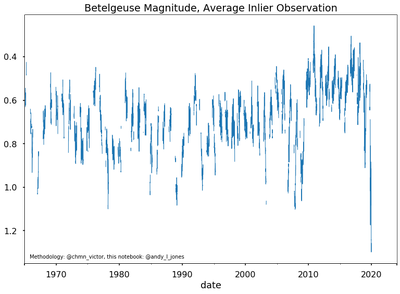
Just prior to the gravity wave burst the star Betelgeuse has undergone some unusual dimming in 2019.
The problem is the people of Ligo could not pin-point the location of the gravity wave burst yet they have stated it may have come from the Orion Constellation where Betelgeuse resides.
Gravity waves when traveling through space do not bend around stars as does light, therefore gravity waves would arrive at earth before a Supernova flash.
Since gravity waves is cutting edge science and not enough data has been retrieved to be compared for lag time of light to a gravity wave arrival time; as this is all theory at the moment trying to predict the speed of lights lag time compared to gravity waves from a distant object in space, I have found a calculation. However, my theory is based on a measurement that Betelgeuse's distance in light years is 535 from the Great Pyramid. Something tells me a very advanced civilization built the pyramids which exceeded our technology and to me it could be extra-terrestrial. Mankind has not been able to approximate Betelgeuse's light year distance properly and there is several speculations of its distance online.

Knowing the exact distance in light years to Betelgeuse is pivotal if one were to predict a Supernova flash shortly from Betelgeuse in the future due to a gravity wave emission. I wrote a program in python which predicts the difference from a gravity wave geometric calculation to light years that maybe able to predict when Betelgeuse goes Supernova if it did indeed explode in 1491. This calculation I came up with .99307 x 535 = 529.84795 from my python program. The lag for the light delay should arrive sometime in March of 2025 knowing that the difference in light years is about 5.15205.
Here is a vid that explains what I have done:
For the below code here is some input information for black holes I used to determine distance from the data at Ligo Labs:
When using my python code you input:
Enter Number to divide Proton: 10000
Spin Number: 1
Enter number of Parsec's for Luminosity Distance: 410
Add Parsec's for Luminosity Distance: 160
Subtract Parsec's for Luminosity Distance: 180
or another one
_______________
Enter Number to divide Proton: 1000000
Spin Number: 8
Enter number of Parsec's for Luminosity Distance: 5300
Add Parsec's for Luminosity Distance: 2400
Subtract Parsec's for Luminosity Distance: 2600
Here is the code I programmed for the gravity geometric in python:
Python:
import time
print('''Two to the power of Exponential growth of Gravities
Constant <G> multiplied by the fine structure contant multiplied
by 12 hours divided by n.
________________________________________ ''')
while True:
n = int(input("Enter Number to divide Proton: "))
s = int(input("Spin Number: "))
Parsec = int(input("Enter number of Parsec's for Luminosity Distance: "))
Plus_Parsec = int(input("Add Parsec's for Luminosity Distance: "))
Minus_Parsec = int(input("Subtract Parsec's for Luminosity Distance: "))
start_time = time.time()
G_constant = (.00000000006674)
proton_width = (((0.00000000000001)*s)/(n))
gravity_wave = ((proton_width))
G = ((pow(2,((1 +(((.00000000006674*.0072973*(12/n))*((( 1 ))))))))))
Gravities_Geometry = ((G*3.14))
Distance_to_Gravity_Waves_Source = ((((((G))/(gravity_wave))*86400*365)/((Gravities_Geometry)-((G/2))))/9461000000000000)
Ligos_approximation_Black_hole_merger_from_luminosity = (1000000*3.26*(Parsec+(Plus_Parsec-Minus_Parsec)))
difference = (Ligos_approximation_Black_hole_merger_from_luminosity-Distance_to_Gravity_Waves_Source)
print('{0:.14f}'.format(G_constant),'Gravitational Constant')
# print('{0:.99f}'.format(proton_width),'Proton Width')
# print('{0:.110f}'.format(gravity_wave),'Gravity Wave')
print(G,'G as exponential growth')
print('{0:.15f}'.format(Gravities_Geometry),'Gravities_Geometry')
print("{:,}".format(Ligos_approximation_Black_hole_merger_from_luminosity),'Ligos distance approximation from luminosity in light years')
print('{0:,.1f}'.format(Distance_to_Gravity_Waves_Source),'Distance Gravity Wave traveled going by ONeils Gravity Geometric')
print("{:,}".format(difference),'difference from Ligo and Geometric source in light years')
e = int(time.time() - start_time)
print('{:02d}:{:02d}:{:02d}'.format(e // 3600, (e % 3600 // 60), e % 60))
@All
I finally found another Gravity Wave Measurement measured against the diameter of the proton. The first gravity wave found was (GW150914) measured at a 10,000th of the diameter of a proton. It had a spin of -.01 and so in my python code it would be a 1 spin. I should explain Luminosity Distance, it is an approximation in the linear direction because light bends around massive objects on its way from deep space to the measuring point. At some junctures light can bend greater than other junctures, because of mass differences and this is why its an approximation for very deep objects. Often times Luminosity will be printed like this:
5300+2400−2600.
So to find the total light years. You would multiply 1,000,000*3.26*(5300+(2400-2600))light years
As I desperately searched the net to see if my Gravity Geometric was correct; I finally stumbled on to an article regarding the gravity wave (GW190521) measured at a 1,000,000th of the diameter of a proton. I then looked at the spin for the GW190521 and it was an .08 and so in my python code it would be an 8 spin which also plays a role in the calculation.
This was great that I found two measurements to test my Gravity Geometric to see how it faired against the approximate luminosity distance measuring stick. And just as I imagined at greater distances than smaller Luminosity as an approximation increases with time, because light bends around other massive objects on its way to where its being measured. On the other hand gravity takes a straight path to the target being measured unhindered by mass. So this is why I'm so excited to show the result. I'm not using Luminosity to show distance and perhaps as I just discussed light not being accurate, that I'm spot on for light years with my Geometric Result.