The source of dark energy is gravitational self-energy or the gravitational action of the gravitational field!
1. Gravitational potential energy is negative energy
1) Alan Guth said
2) Stephen Hawking also said
Both said that gravitational potential energy is negative energy and is the true energy that can cancel positive mass energy.
3) Negative energy (mass) density in standard cosmology
From the second Friedmann equation or acceleration equation,
(1/R)(d^2R/dt^2)=-(4πG/3)(ρ+3P)
In standard cosmology, it is explained by introducing an entity that has a positive mass density but exerts a negative pressure.
p + 3P = p + 3(-p) = - 2p
However, If we rearrange the dark energy term, the final result is a negative mass density of -2p.
In the standard cosmology, accelerated expansion is impossible without negative mass density. It is just that the negative mass density term is called negative pressure, so it is not recognized.
4) Gravitational binding energy and mass defect
https://en.wikipedia.org/wiki/Gravitational binding energy
5) Since gravitational self-energy is proportional to -M^2/R, The greater the mass, the greater the gravitational self-energy ratio
In the dimensional analysis of energy, E has kg(m/s)^2, so all energy can be expressed in the form of (mass) x (speed)^2. So, E=Mc^2 holds true for all kinds of energy. "-M_gs" is the equivalent mass of gravitational self-energy. It is a negative equivalent mass term.
Earth's -M_gs = (- 4.17x10^-10)M_Earth
Sun's -M_gs = (- 1.27x10^-4)M_Sun
Black hole's -M_gs = (- 0.3)M_Black-hole
For example, in the case of a black hole,
-M_gs=-(3/5)(GM^2)/(Rc^2)=-(3/5)(GM^2)/((2GM/c^2)c^2)=-(3/10)M=-0.3M_Black-hole
What about the universe with more mass?
2. In the universe, if we calculate the gravitational self-energy or total gravitational potential energy
The universe is almost flat, and its mass density is also very low. Thus, Newtonian mechanics approximation can be applied.
Since the particle horizon is the range of interaction, if we find the Mass energy (Mc^2) and Gravitational self-energy ((-M_gs)c^2) values at each particle horizon, Mass energy is an attractive component, and the equivalent mass of gravitational self-energy is a repulsive component. Critical density value p_c = 8.50 x 10^-27[kgm^-3] was used.
At particle horizon R=16.7Gly, (-M_gs)c^2 = (-0.39M)c^2 : |(-M_gs)c^2| < (Mc^2) : Decelerated expansion period
At particle horizon R=26.2Gly, (-M_gs)c^2 = (-1.00M)c^2 : |(-M_gs)c^2| = (Mc^2) : Inflection point (About 5-7 billion years ago, consistent with standard cosmology.)
At particle horizon R=46.5Gly, (-M_gs)c^2 = (-3.04M)c^2 : |(-M_gs)c^2| > (Mc^2) : Accelerated expansion period
Even in the universe, gravitational potential energy (or gravitational action of the gravitational field) must be considered.
And, in fact, if we calculate the value, since gravitational self-energy is larger than mass energy, so the universe has accelerated expansion.
Gravitational self-energy accounts for decelerated expansion, inflection point, and accelerated expansion.
3. New Friedmann's equations and the dark energy term from the gravitational self-energy model



Finding the dark energy term with this model is similar to the standard cosmology value.
Gravitational potential energy is a concept that has already existed, and does not assume a bizarre existence that has a positive inertial mass and exerts a negative pressure. There are no problems like fine tuning or CCC problem.
In standard cosmology, the energy density of dark energy is a constant. However, in the gravitational self-energy model, dark energy density is a variable.
The dark energy (or cosmological constant term) is a function of time. Thus, this model can be verified.
# Dark energy is the Gravitational Potential Energy or Gravitational Self-Energy
https://www.researchgate.net/publication/360096238
1. Gravitational potential energy is negative energy
1) Alan Guth said
The energy of a gravitational field is negative!
The positive energy of the false vacuum was compensated by the negative energy of gravity.
2) Stephen Hawking also said
The matter in the universe is made out of positive energy. However, the matter is all attracting itself by gravity. Two pieces of matter that are close to each other have less energy than the same two pieces a long way apart, because you have to expend energy to separate them against the gravitational force that is pulling them together. Thus, in a sense, the gravitational field has negative energy. In the case of a universe that is approximately uniform in space, one can show that this negative gravitational energy exactly cancels the positive energy represented by the matter. So the total energy of the universe is zero.
Both said that gravitational potential energy is negative energy and is the true energy that can cancel positive mass energy.
3) Negative energy (mass) density in standard cosmology
From the second Friedmann equation or acceleration equation,
(1/R)(d^2R/dt^2)=-(4πG/3)(ρ+3P)
In standard cosmology, it is explained by introducing an entity that has a positive mass density but exerts a negative pressure.
p + 3P = p + 3(-p) = - 2p
However, If we rearrange the dark energy term, the final result is a negative mass density of -2p.
In the standard cosmology, accelerated expansion is impossible without negative mass density. It is just that the negative mass density term is called negative pressure, so it is not recognized.
4) Gravitational binding energy and mass defect
https://en.wikipedia.org/wiki/Gravitational binding energy
Two bodies, placed at the distance R from each other and reciprocally not moving, exert a gravitational force on a third body slightly smaller when R is small. This can be seen as a negative mass component of the system, equal, for uniformly spherical solutions, to:
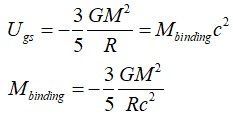
5) Since gravitational self-energy is proportional to -M^2/R, The greater the mass, the greater the gravitational self-energy ratio
In the dimensional analysis of energy, E has kg(m/s)^2, so all energy can be expressed in the form of (mass) x (speed)^2. So, E=Mc^2 holds true for all kinds of energy. "-M_gs" is the equivalent mass of gravitational self-energy. It is a negative equivalent mass term.
Earth's -M_gs = (- 4.17x10^-10)M_Earth
Sun's -M_gs = (- 1.27x10^-4)M_Sun
Black hole's -M_gs = (- 0.3)M_Black-hole
For example, in the case of a black hole,
-M_gs=-(3/5)(GM^2)/(Rc^2)=-(3/5)(GM^2)/((2GM/c^2)c^2)=-(3/10)M=-0.3M_Black-hole
What about the universe with more mass?
2. In the universe, if we calculate the gravitational self-energy or total gravitational potential energy
The universe is almost flat, and its mass density is also very low. Thus, Newtonian mechanics approximation can be applied.
Since the particle horizon is the range of interaction, if we find the Mass energy (Mc^2) and Gravitational self-energy ((-M_gs)c^2) values at each particle horizon, Mass energy is an attractive component, and the equivalent mass of gravitational self-energy is a repulsive component. Critical density value p_c = 8.50 x 10^-27[kgm^-3] was used.
At particle horizon R=16.7Gly, (-M_gs)c^2 = (-0.39M)c^2 : |(-M_gs)c^2| < (Mc^2) : Decelerated expansion period
At particle horizon R=26.2Gly, (-M_gs)c^2 = (-1.00M)c^2 : |(-M_gs)c^2| = (Mc^2) : Inflection point (About 5-7 billion years ago, consistent with standard cosmology.)
At particle horizon R=46.5Gly, (-M_gs)c^2 = (-3.04M)c^2 : |(-M_gs)c^2| > (Mc^2) : Accelerated expansion period
Even in the universe, gravitational potential energy (or gravitational action of the gravitational field) must be considered.
And, in fact, if we calculate the value, since gravitational self-energy is larger than mass energy, so the universe has accelerated expansion.
Gravitational self-energy accounts for decelerated expansion, inflection point, and accelerated expansion.
3. New Friedmann's equations and the dark energy term from the gravitational self-energy model

Finding the dark energy term with this model is similar to the standard cosmology value.
Gravitational potential energy is a concept that has already existed, and does not assume a bizarre existence that has a positive inertial mass and exerts a negative pressure. There are no problems like fine tuning or CCC problem.
In standard cosmology, the energy density of dark energy is a constant. However, in the gravitational self-energy model, dark energy density is a variable.
The dark energy (or cosmological constant term) is a function of time. Thus, this model can be verified.
# Dark energy is the Gravitational Potential Energy or Gravitational Self-Energy
https://www.researchgate.net/publication/360096238
Last edited:


