Solution to singularity problem, Solution to infinite density problem!
The biggest problem with black holes is the singularity problem. This singularity denies application of the existing laws of physics and it is unnatural for a certain substantial object to have infinite density of energy. Besides, such singularity has never been observed as substance but is just a mathematical result of general relativity, which is considered a defect or limit of the theory.
Although it is generally thought that the singularity problem can be solved by quantum mechanics, it is possible that this singularity problem can be solved by gravitational potential energy or gravitational binding energy.
1.Gravitational self-energy (or gravitational binding energy) and mass defect effect
The concept of gravitational self-energy(U_gs) is the total of gravitational potential energy possessed by a certain object M itself. Since a certain object M itself is a binding state of infinitesimal mass dMs, it involves the existence of gravitational potential energy among these dMs and is the value of adding up these. M = ΣdM. The gravitational self-energy is equal to the minus sign of the gravitational binding energy. Only the sign is different because it defines the gravitational binding energy as the energy that must be supplied to the system to bring the bound object into a free state.

U_gs = -(3/5)(GM^2)/R
https://en.wikipedia.org/wiki/Gravitational_binding_energy
In the case of a spherical uniform distribution, the total energy of the system, including gravitational potential energy, is
E_T=Σ(m_i)c^2 - Σ-G(m_i)(m_j)/r = Mc^2 - (3/5)(GM^2)/R
In the general case, the value of total gravitational potential energy (gravitational self-energy) is small enough to be negligible, compared to mass energy Mc^2. So generally, there was no need to consider gravitational potential energy. However, as R gets smaller, the absolute value of U_gs increases. For this reason, we can see that U_gs is likely to offset the mass energy in a certain radius. The mass defect effect due to binding energy has already been demonstrated in particle physics.
If we calculate the values of the total gravitational potential energy of celestial bodies, we get surprising results.

It can be seen that the total gravitational potential energy is 1/10000 of the mass energy in the case of the sun and 30% of the mass of the black hole at the event horizon of the black hole.
2.Solving the Singularity Problem of Black Hole
Looking for the size in which negative gravitational self-energy becomes equal to positive mass energy by comparing both,

This equation means that if mass M is uniformly distributed within the radius R_gs, gravitational self-energy for such an object equals mass energy in size. So, in case of such an object, (positive) mass energy and (negative) gravitational self-energy can be completely offset while total energy is zero. Since total energy of such an object is 0, gravity exercised on another object outside is also 0.
Comparing R_gs with R_S, the radius of Schwarzschild black hole,

This means that there exists the point where gravitational self-energy (- gravitational binding energy) becomes equal to mass energy within the radius of black hole, and that, supposing a uniform distribution, the value exists at the point 0.3R_S, about 30% level of the black hole radius.
When applying the Viral theorem, this value is halved. R_gs-vir=0.15R_S
The area of within R_gs has gravitational self-energy(gravitational potential energy) of negative value, which is larger than mass energy of positive value. If r (radius of mass distribution) is less than R_gs, this area becomes negative energy (mass) state. There is a repulsive gravitational effect between the negative masses, which causes it to expand again.
From the equation above, even if some particle comes into the radius of black hole, it is not a fact that it contracts itself infinitely to the point R = 0. From the point R_gs, gravity is 0, and when it enters into the area of R_gs, total energy within R_gs region corresponds to negative values enabling anti-gravity to exist. This R_gs region comes to exert repulsive effects of gravity on the particles outside of it, therefore it interrupting the formation of singularity at the near the area R = 0
If you have only the concept of positive energy, please refer to the following explanation.
The total energy of the system, including gravitational potential energy, is
E_T=Σ(m_i)c^2 - Σ-G(m_i)(m_j)/r = Mc^2 - (3/5)(GM^2)/R
From the point of view of mass defect, r=R_gs is the point where the total energy of the system is zero. For the system to compress more than this point, there must be an positive energy release from the system. However, since the total energy of the system is zero, there is no positive energy that the system can release. Therefore, the system cannot be more compressed than r=R_gs. So black hole doesn't have singularity.
In case of the smallest stellar black hole with three times the solar mass, R_S = 9km. R_gs of this object is as far as 3km. In other words, even in a black hole with smallest size that is made by the gravitational contraction of a star, the distribution of internal mass can’t be reduced below radius 3km.
Before reaching the quantum mechanical scale, the singularity problem is solved by gravity itself.
3.Internal structure of a black hole according to this model
By competing between the (negative) gravitational self-energy and the (positive) mass energy, particles inside black hole or distribution of energy can be stabilized. As a final state, the black hole does not have a singularity in the center, but it has a zero (total) energy zone.
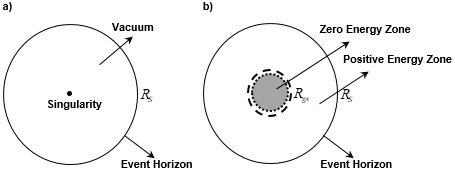
Internal structure of the black hole. a)Existing model b)New model.
If, over time, the black hole stabilizes, the black hole does not have a singularity in the center, but it has a zero (total) energy zone. Since there is a repulsive gravitational effect between negative energies (masses), the mass distribution expands, and when the mass distribution expands, the magnitude of the negative gravitational self-energy decreases, so it enters the positive energy state again. Therefore, finally, the mass distribution is stabilized at zero total energy.
4. The gravitational singularity can be solved by gravity, not by quantum mechanics
Think about a black hole with the size 10 billion times bigger than the solar mass. Schwarzschild radius of this black hole is R_S = 3 × 10^10 km and R_gs of this black hole 1 × 10^10 km. Average density of this black hole is about 1.81kg/m^3. And average density of the Earth is about 5, 200kg/m^3.
Is it a size that requires quantum mechanics? Is it a high density state that requires quantum mechanics? Black hole of this size is Newtonian mechanics’ object and therefore, gravitational potential energy must be considered.
Let’s reduce the mass of this black hole gradually and approach three times the solar mass, the smallest size of black hole where stars can be formed! In case of the smallest black hole with three times the solar mass, R_S = 9km. R_gs of this object is as far as 3km. In other words, even in a black hole with smallest size that is made by the contraction of a star, the distribution of internal mass can’t be reduced to at least radius 3km (Rgs−vir = 1.5km). Before reaching the quantum mechanical scale, the singularity problem is solved
5.Minimum size of existence
[ Existence = the sum of infinitesimal existences composing an existence ]
A single mass M for some object means that it can be expressed as M = ∑ dM and, for energy, E = ∑ dE. The same goes for elementary particles, which can be considered a set of dMs, the infinitesimal mass.
R_gs equation means that if masses are uniformly distributed within the radius R_gs, the size of negative binding energy becomes equal to that of mass energy. This can be the same that the rest mass, which used to be free for the mass defect effect caused by binding energy, has all disappeared. This means the total energy value representing “some existence” coming to 0 and “extinction of the existence”. Therefore, R_gs is considered to act as “the minimal radius” or “a bottom line” of existence with some positive energy.
R_min = R_gs = (3/5)GM/c^2
*In the case of entities with negative energy, since the gravitational properties are repulsive, the mass distribution expands until the negative energy state is resolved.
**The position-momentum uncertainty principle also gives limits on the size limit, but when considering infinitely large momentum, there is no minimum radius. On the other hand, gravitational self-energy gives a minimum radius due to the presence of energy.
#Paper
Solution of the Singularity Problem of Black Hole
The biggest problem with black holes is the singularity problem. This singularity denies application of the existing laws of physics and it is unnatural for a certain substantial object to have infinite density of energy. Besides, such singularity has never been observed as substance but is just a mathematical result of general relativity, which is considered a defect or limit of the theory.
The prediction of singularities undoubtedly represents a breakdown of general relativity in that its classical description of gravitation - Wald. General Relativity Book.
Although it is generally thought that the singularity problem can be solved by quantum mechanics, it is possible that this singularity problem can be solved by gravitational potential energy or gravitational binding energy.
1.Gravitational self-energy (or gravitational binding energy) and mass defect effect
The concept of gravitational self-energy(U_gs) is the total of gravitational potential energy possessed by a certain object M itself. Since a certain object M itself is a binding state of infinitesimal mass dMs, it involves the existence of gravitational potential energy among these dMs and is the value of adding up these. M = ΣdM. The gravitational self-energy is equal to the minus sign of the gravitational binding energy. Only the sign is different because it defines the gravitational binding energy as the energy that must be supplied to the system to bring the bound object into a free state.
U_gs = -(3/5)(GM^2)/R
https://en.wikipedia.org/wiki/Gravitational_binding_energy
In the case of a spherical uniform distribution, the total energy of the system, including gravitational potential energy, is
E_T=Σ(m_i)c^2 - Σ-G(m_i)(m_j)/r = Mc^2 - (3/5)(GM^2)/R
In the general case, the value of total gravitational potential energy (gravitational self-energy) is small enough to be negligible, compared to mass energy Mc^2. So generally, there was no need to consider gravitational potential energy. However, as R gets smaller, the absolute value of U_gs increases. For this reason, we can see that U_gs is likely to offset the mass energy in a certain radius. The mass defect effect due to binding energy has already been demonstrated in particle physics.
If we calculate the values of the total gravitational potential energy of celestial bodies, we get surprising results.
It can be seen that the total gravitational potential energy is 1/10000 of the mass energy in the case of the sun and 30% of the mass of the black hole at the event horizon of the black hole.
2.Solving the Singularity Problem of Black Hole
Looking for the size in which negative gravitational self-energy becomes equal to positive mass energy by comparing both,
This equation means that if mass M is uniformly distributed within the radius R_gs, gravitational self-energy for such an object equals mass energy in size. So, in case of such an object, (positive) mass energy and (negative) gravitational self-energy can be completely offset while total energy is zero. Since total energy of such an object is 0, gravity exercised on another object outside is also 0.
Comparing R_gs with R_S, the radius of Schwarzschild black hole,
This means that there exists the point where gravitational self-energy (- gravitational binding energy) becomes equal to mass energy within the radius of black hole, and that, supposing a uniform distribution, the value exists at the point 0.3R_S, about 30% level of the black hole radius.
When applying the Viral theorem, this value is halved. R_gs-vir=0.15R_S
The area of within R_gs has gravitational self-energy(gravitational potential energy) of negative value, which is larger than mass energy of positive value. If r (radius of mass distribution) is less than R_gs, this area becomes negative energy (mass) state. There is a repulsive gravitational effect between the negative masses, which causes it to expand again.
From the equation above, even if some particle comes into the radius of black hole, it is not a fact that it contracts itself infinitely to the point R = 0. From the point R_gs, gravity is 0, and when it enters into the area of R_gs, total energy within R_gs region corresponds to negative values enabling anti-gravity to exist. This R_gs region comes to exert repulsive effects of gravity on the particles outside of it, therefore it interrupting the formation of singularity at the near the area R = 0
If you have only the concept of positive energy, please refer to the following explanation.
The total energy of the system, including gravitational potential energy, is
E_T=Σ(m_i)c^2 - Σ-G(m_i)(m_j)/r = Mc^2 - (3/5)(GM^2)/R
From the point of view of mass defect, r=R_gs is the point where the total energy of the system is zero. For the system to compress more than this point, there must be an positive energy release from the system. However, since the total energy of the system is zero, there is no positive energy that the system can release. Therefore, the system cannot be more compressed than r=R_gs. So black hole doesn't have singularity.
In case of the smallest stellar black hole with three times the solar mass, R_S = 9km. R_gs of this object is as far as 3km. In other words, even in a black hole with smallest size that is made by the gravitational contraction of a star, the distribution of internal mass can’t be reduced below radius 3km.
Before reaching the quantum mechanical scale, the singularity problem is solved by gravity itself.
3.Internal structure of a black hole according to this model
By competing between the (negative) gravitational self-energy and the (positive) mass energy, particles inside black hole or distribution of energy can be stabilized. As a final state, the black hole does not have a singularity in the center, but it has a zero (total) energy zone.
Internal structure of the black hole. a)Existing model b)New model.
If, over time, the black hole stabilizes, the black hole does not have a singularity in the center, but it has a zero (total) energy zone. Since there is a repulsive gravitational effect between negative energies (masses), the mass distribution expands, and when the mass distribution expands, the magnitude of the negative gravitational self-energy decreases, so it enters the positive energy state again. Therefore, finally, the mass distribution is stabilized at zero total energy.
4. The gravitational singularity can be solved by gravity, not by quantum mechanics
Think about a black hole with the size 10 billion times bigger than the solar mass. Schwarzschild radius of this black hole is R_S = 3 × 10^10 km and R_gs of this black hole 1 × 10^10 km. Average density of this black hole is about 1.81kg/m^3. And average density of the Earth is about 5, 200kg/m^3.
Is it a size that requires quantum mechanics? Is it a high density state that requires quantum mechanics? Black hole of this size is Newtonian mechanics’ object and therefore, gravitational potential energy must be considered.
Let’s reduce the mass of this black hole gradually and approach three times the solar mass, the smallest size of black hole where stars can be formed! In case of the smallest black hole with three times the solar mass, R_S = 9km. R_gs of this object is as far as 3km. In other words, even in a black hole with smallest size that is made by the contraction of a star, the distribution of internal mass can’t be reduced to at least radius 3km (Rgs−vir = 1.5km). Before reaching the quantum mechanical scale, the singularity problem is solved
5.Minimum size of existence
[ Existence = the sum of infinitesimal existences composing an existence ]
A single mass M for some object means that it can be expressed as M = ∑ dM and, for energy, E = ∑ dE. The same goes for elementary particles, which can be considered a set of dMs, the infinitesimal mass.
R_gs equation means that if masses are uniformly distributed within the radius R_gs, the size of negative binding energy becomes equal to that of mass energy. This can be the same that the rest mass, which used to be free for the mass defect effect caused by binding energy, has all disappeared. This means the total energy value representing “some existence” coming to 0 and “extinction of the existence”. Therefore, R_gs is considered to act as “the minimal radius” or “a bottom line” of existence with some positive energy.
R_min = R_gs = (3/5)GM/c^2
*In the case of entities with negative energy, since the gravitational properties are repulsive, the mass distribution expands until the negative energy state is resolved.
**The position-momentum uncertainty principle also gives limits on the size limit, but when considering infinitely large momentum, there is no minimum radius. On the other hand, gravitational self-energy gives a minimum radius due to the presence of energy.
#Paper
Solution of the Singularity Problem of Black Hole


